The pv( function (short for present value) calculates the present value of an income or debit stream of payments.
Parameters
This function has five parameters:rate – is the interest rate of the investment (per period). For example, if there is one payment per year, this is the annual percentage rate. If there is one payment per month, then this is the monthly percentage rate.
periods – is the number of payments that will be made during the life of the investment. For example, if this is a 36-month investment with one payment per month, this value is 36. If this is a 30-year investment with one payment per month this value is 360.
payment – is the amount being invested each period. If this is money that is coming to you this value should actually be negative. For example, if you are receiving $500 per month, the payment amount should be -500.
balloon – (future value) is any lump sum payment at the end of the investment (actually the negative of the balloon payment). For example if you are receiving $25,000 at the end of ten years, this value should be -25000.
begin – specifies whether payments are made at the beginning (1) or end of each period (0).
Description
The pv( function (short for present value) calculates the present value of an income or debit stream of payments. Present value is an economic calculation that is the equivalent of a bird in the hand is worth two in the bush, or is that a bird in the hand worth 1.67 in the bush? It’s better to receive $1000 right now than $1000 next year, but how much better? The pv( function will tell you.
If the payment period is annual, the calculation is simple. Suppose someone offers to pay you either $2,500 right now, or $1000 per year for the next three years. Which should you take? The answer depends on the interest rate you can get for your money (and, of course, how much you need cash now, but that’s another question). If you can invest your money at 7% then the three payments are worth $2624 now (see below), but if you can get 10%, then three payments later are only worth $2486 now.
pv(.07,3,-1000,0,0) ☞ 2624.32
pv(.10,3,-1000,0,0) ☞ 2486.85
Most investments are paid more frequently than once a year - usually once a month. To calculate the present value for such an investment, you must convert the annual percentage rate into a monthly percentage rate by dividing by 12. Suppose someone offers you $200 a month at the beginning of each month for 5 years, and you know that you can put your money into an investment that returns 13.5% annual interest. What is the cash payment that would be equivalent to that income stream?
pv(0.135/12,5*12,-200,0,1) ☞ 8789.72
You can also use this function to calculate the current value of a single balloon payment, with no payments. Suppose someone offers to pay you $50,000 5 years from now. You know that you can invest your money at 14% annual interest. This formula will calculate the value of the equivalent cash value of this $50,000 future payment ($25,968) :
pv(0.14,5,0,-50000,0) ☞ 25968.40
Of course the pv( function only works with fixed interest rates.
Here is the formula that Panorama uses to calculate present value.
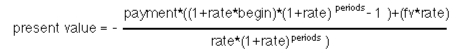
Note: The pv( function is designed to be compatible with the Microsoft Excel function of the same name.
See Also
- fv( -- (short for *future value*) calculates the future value of an investment.
- pmt( -- (short for *payment*) calculates the periodic payment required to pay off a loan.
History
| Version | Status | Notes |
| 10.0 | No Change | Carried over from Panorama 6.0 |